ICFPC — это ежегодное трёхдневное соревнование по программированию. Задачи всегда «жизненные» в том смысле, что они не сводятся к какому-то конкретному алгоритму; приходится выдумывать эвристики, комбинировать подходы, а кое-где даже подправлять руками. Как и в жизни, задание каждый день обрастает новыми требованиями и нюансами. Скучно не бывает почти никогда.

В этом году контест был для меня юбилейным — я участвовал в десятый раз. ICFPC сразу стал и до сих пор остаётся хайлайтом моего года: я стараюсь взять отпуск и прошу домашних не беспокоить меня, если только не случится пожар или потоп. Вишенкой на этом торте выступает команда, остов которой не меняется все эти годы.

Хронологию уже расписал в своём отчёте Форневер, а я расскажу пару анекдотов о самых драйвовых моментах этого года. Пост Форневера лучше прочитать сейчас, потому что я не буду пересказывать условия задач, а сразу нырну в глубокие детали.

Обед пятницы начался, конечно же, с чтения спецификации (зеркало), и на первый взгляд она показалось унылой: снова отсылки к предыдущим годам, снова доморощенный Лисп с надуманным кодированием, снова оптимизационная задача. В этот раз нужно было обойти поле для игры LambdaMan (аналог Pacman) за минимальное количество шагов. Скукотень! Чтобы хоть как-то развлечься, я сел писать интерпретатор этого их «космолиспа», а Портнов взялся за парсинг.

Он де Бружин, а не де Бриён!

Парсить и интерпретировать лисп довольно просто, и спустя каких-то пять часов мы уже вычисляли все примеры из спецификации. Но все равно вляпались. Одним из заданий было вычисление большой программы под названием language_test, и на ней наш интерпретатор выдавал ошибку. Собственно, это сама программа прямым текстом сообщала, что пошло не так: «application is not correct». «Application» это не «приложение», а «применение функции». Пока я ужинал, Портнов докопался до первопричины — при вычислениях мы не переименовывали переменные.

В «космолиспе» — так мы прозвали этот их диалект лиспа в честь задания 2020-го года — у лямбда-выражения ровно один аргумент. Применить лямбду к конкретному значению очень просто: берём её тело, вместо переменной подставляем аргумент, и всё — получившееся выражение и есть результат применения. Если записать этот процесс синтаксисом Haskell, то получится вот так:

(\x -> x + x) 4
= 4 + 4
= 8

Проблема возникает, если внутри лямбды лежит другая лямбда, использующая такое же имя переменной. Переменная во внутренней лямбде должна «затенять» наружную переменную, а если подставлять наивно, то результат получается неправильным:

((\x -> (\x -> x + x)) 3) 4
= (\x -> 3 + 3) 4
= 3 + 3
= 6

Если переименовать переменные, то выражение будет вычислено правильно:

((\x -> (\y -> y + y)) 3) 4
= (\y -> y + y) 4
= 4 + 4
= 8

Вот на этом-то и прокололся наш интерпретатор: он не переименовывал переменные и выдавал неверные ответы. Для решения этой проблемы есть хитрый алгоритм, но мы с Портновым придумали другой (кто не боится Haskell — смотрите вот сюда):

1. найти переменную с «наибольшим» именем (в «космолиспе» переменные обозначаются номерами, так что это было легко). Мы будем нумеровать новые переменные так, чтобы их номера не пересекались с уже существующими;
2. рекурсивно спускаться по дереву и:
   1. если встретили лямбду — пушнуть на стек номер её переменной вместе с новым номером (которые генерируются последовательно);
   2. если встретили переменную — искать её номер в стеке, начиная сверху, и заменить на найденный новый номер;
   3. если вышли из лямбды — удалить верхнее значение из стека.

(\x -> (\y -> x*y)) 2
= (\y -> 2*y)

Свой долг перед WinRar считаю искупленным

ожидание: весело пишем на Хаскеле

реальность: весело пишем на Хаскеле сначала Лисп, потом дебаг-тулы для Лиспа, потом уже на нём чуть менее весело пишем решение задачи и дебажим

Решения для карт LambdaMan оценивались не по количеству сделанных шагов, а по размеру сабмита. Сабмитили мы программы на «космолиспе», так что, выходит, эти задачи были не про оптимальный обход, а про написание наименьшей возможной программы, которая напечатает решение! Очевидно, нужно было сжать решение с помощью run-length encoding, но я стушевался, не придумав подходящего формата для хранения результата. Мне виделась необходимость в списках пар, а кодирование этого на «космолиспе» было бы весьма накладным.

Поэтому я придумал вариант попроще: каждому из четырёх возможных движений сопоставить цифру пятеричной системы счисления и кодировать путь Пакмана длинным пятеричным числом. Пятый символ нужен для того, чтобы кодировать первое движение в самом начале решения; если бы оно кодировалось нулём, то пятеричное число в начале кодирования не менялось бы. Естественно, частью нашего сабмишена должен быть распаковщик, позволяющий декодировать число обратно в строку.

Идея простая, но чтобы написать декодер на чистом лямбда-исчислении, пришлось попотеть. Цитата в начале этого раздела как раз о моих впечатлениях от этого процесса. Позже я ещё оптимизировал решение: начал вместе с числом отправлять ещё и длину решения, что позволило испольовать в кодировании ноль и перейти на число по основанию 4. К моему удивлению, так даже декодер получился меньше. RLE попозже реализовал Портнов.

Никаких выводов из этого опыта я, конечно же, не сделал, потому что тут же занялся по сути похожей, но гораздо более сложной задачей: efficiency.

Оптимизирующие компиляторы не нужны!

Как и Форневер, я получил уйму кайфа от решения задачек из курса efficiency. Мы сразу догадались, что нужно будет вычислять какие-то адски сложные выражения. Понимание, что такое «адски» по меркам ICFPC, пришло к нам чуть позже.

Первое задание возводило 4 в большую степень, при этом умножение было реализовано через сложение: аргумент складывался сам с собой четыре раза. Как я уже рассказал, лямбды вычисляются подстановкой переменной, поэтому лямбда-выражение \x -> x + x + x + x, применённое к безобидному 1+2+3, превращается в 1+2+3 + 1+2+3 + 1+2+3 + 1+2+3. Это называется call-by-name и отличается от гораздо более популярного call-by-value, где аргумент сначала вычисляется, а потом уже передаётся в функцию. Из-за call-by-name и большого количества применений функции эта программа сожрала бы всю память до того, как завершилась бы, поэтому я посчитал её результат в калькуляторе.

Второе задание умножало большое сложное выражение на ноль. Это был единственный случай, когда выражение можно было посчитать с помощью нашего интерпретатора — достаточно было перед вычислением аргументов проверить, не равен ли один из них литералу 0.

Третье задание считало (рекурсивно) от одного до 9 345 873 500, после чего прибавляло к результату 2 134. Сложно для компьютера, элементарно для человека.

Четвёртое привело меня в экстаз (я не преувеличиваю!). Благодаря предыдущим задачам я уже приноровился видеть в коде так называемый Y-комбинатор, с помощью которого можно зациклить рекурсивную функцию. Меня настолько прёт, что я вам сейчас всё про это расскажу! (Но вы можете пролистать, я не обижусь.)

pow :: Integer -> Integer -> Integer
pow x n =
    if n == 0
    then 1
    else x * pow x (n-1)

(lambda (pow)
  (lambda (x)
    (lambda (n)
      (if
        (= n 0)
        1
        (* x (((pow pow) x) (- n 1)))))))

(lambda (pow)
  (lambda (x)
    (lambda (n)
      (((pow pow)
          x)
        n))))

; Теперь сюда будет передаваться не копия этой функции,
; а её версия, где первый аргумент уже применён.
(lambda (self)
  (lambda (x)
    (lambda (n)
      (if
        (= n 0)
        1
        (* x
          ; Соответственно, здесь уже не нужно
          ; передавать self в self
          ((self x) (- n 1)))))))

(lambda (x) (x x))

((lambda (x) (x x))
  (lambda (x) (x x)))

(lambda (f)
  ((lambda (x) (f (x x)))
    (lambda (x) (f (x x)))))

О чём это я?.. А, да, четвёртое задание efficiency. Распарсив его код и выведя на экран AST, я первым делом увидел Y-комбинатор, а остальное было делом техники: по телу лямбды, к которой он применялся, стало понятно, что вычисляются числа Фибоначчи, и я решил задание, просто загуглив нужный элемент последовательности.

Пятую и последующие задачи так легко было не решить, поэтому я махнул рукой и пошёл заниматься 3D-интерпретатором.

DDT

DDT — это когда ты сначала пишешь неправильные тесты, а потом вырываешь волосы, когда корректная имплементация их не проходит. Отличается от TDD тем, что основная масса страданий происходит на этапе имплементации, а не этапе написания тестов, поэтому разработчики воспринимают DDT как «настоящее программирование».

</sarcasm>

Короче, 3D-интерпретатор не проходил часть тестов из-за того, что в тестах был перепутан порядок аргументов в 3D-программе.

Помимо исправления этой маленькой оплошности, я перевёл интерпретатор на стек из монад State и Either, но это чисто технический момент — кодить было весело, а рассказать, по сути, нечего. Почитайте «Haskell in Depth» Брагилевского, там и не такому научитесь!

Решаем задачи нейронкой Gsomix

Последние задания efficiency выглядели совсем непонятно: куча каких-то делений, модулей, условий… Пока я занимался 3D-интерпретатором, Портнов разобрался, что деления и модули — это переход в девятеричную систему счисления, а условия создают ограничения на отдельные разряды получившегося числа. Это выглядело очень похоже на SAT; я уже занимался таким в 2021-м году, а Форневер — в этом. Правда, тут переменные были численными, а не булевыми, поэтому это не SAT, а её обобщение — satisfiability modulo theories (SMT). Для решения таких задач, конечно же, существуют готовые инструменты, поэтому мы с Портновым стали разбираться, какой солвер взять, как донести до него условия задач и как получить ответ.

Первым делом нашёлся Z3, о котором я даже где-то слышал, но никогда не использовал. На вход он требовал формат SMT-LIB, очень похожий на Лисп. Это было нам на руку; я без труда накидал форматилку, превращающую «космолисп» в условие SMT-LIB. Оставалось только объявить переменные и попросить решение. Выглядит это примерно так:

(declare-const n11 Int)
(assert (> n11 0))
(assert (< n11 10))
(declare-const n12 Int)
(assert (> n12 0))
(assert (< n12 10))
(declare-const n13 Int)
(assert (> n13 0))
(assert (< n13 10))
...
(assert
  <здесь большое условие, связывающее разряды девятеричного числа>)
(check-sat)
(get-objectives)

Солвер за полсекунды находил решение, но беда в том, что нам нужно было не какое-нибудь, а минимальное — исходная программа на «космолиспе» начинала перебор с единицы и останавливалась на первом подходящем числе. Форневер в SAT просто выставлял верхние биты руками по мере того, как находил для них решение; на StackOverflow советовали делать то же самое с помощью Z3Py. Мне это показалось костылями, поэтому я почитал документацию и обнаружил, что в Z3 есть директива minimize, которой можно передать критерий для минимизации. Записав туда формулу перехода из девятичной записи в десятичную, я за десяток секунд решил одну из задач.

Следующая, хоть на вид и была аналогична только что решённой, не поддавалась. Пока Z3 шуршал моим процессором, я стал разглядывать условия и внезапно допёр: это же судоку! n11, n12 и т.д. — это n<номер строки><номер столбца>, а огромное условие — это стандартные ограничения судоку плюс несколько начальных цифр. В одной из оставшихся задач начальных ограничений вообще не было, вот она и считалась так долго.

Я предположил, что нам придётся написать для решения полноценный переборщик. Портнов ответил, что лучше написать солвер конкретно для судоку. А Гсомикс предложил заполнить первую строку цифрами 123456789 — это даст минимально возможное число. Пока я это кодировал, Гсомикс придумал, что записать во вторую и третью строки. В итоге с тремя строками Z3 нашёл решение за полторы минуты, с двумя — за 2, с одной — за 11.5, а без предварительно заполненных строк вообще не завершился. Наверное, если бы я чуть медленнее кодировал, Гсомикс решил бы задачки и безо всяких Z3.

В этот момент я уверовал, что за нейронками будущее.

Выводы

Чрезвычайно доволен. Это был один из лучших ICFPC за всё время моего участия. Очень понравилось, что в рамках одного контеста предлагалось несколько разноплановых задач и была возможность переключаться, если застряёшь или просто хочешь отвлечься. В этот раз, например, я почти не прикасался к LambdaMan и Spaceships, и все равно получил море фана.

Очень доволен командой. В этом году мы довольно мало распылялись по языкам, основная часть всё-таки была на Haskell. Кстати, весь наш код можно найти на GitHub.

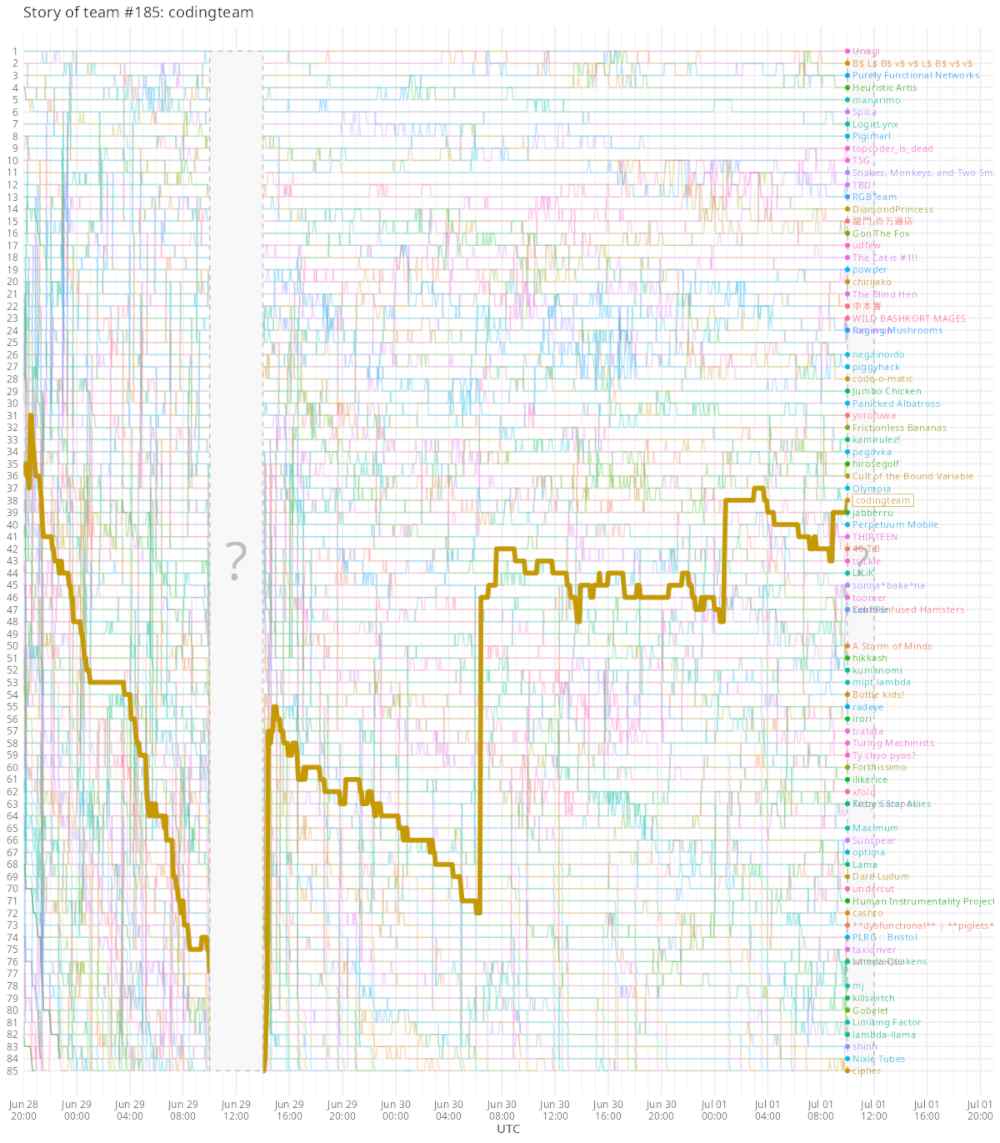
Наконец, доволен итоговым результатом — мы 37-е из 355-и участвовавших (зеркало). Могём! (Особенно если задача прёт.) Вот так выглядело наше путешествие по скорборду:

Если вы дочитали до этого места, значит, ICFPC — это ваше. Будет приятно посоревноваться с вами в следующем году. До встречи!